Zaman 2

I-1 Görelilik Kuramı’nda Zamanın Mutlaklığının Yitişi

Tüm eylemsiz referans çerçevelerinde [0] ışık hızının aynı büyüklükte olduğunu ve fizik yasalarının benzer şekilde işlediğini belit kabul eden Özel Görelilik Kuramı zaman ve mekanın birbirinden ayrık düşünülemeyeceği bir doğa kurgusu gerektiriyor. Burdan yola çıkarak, kuram zamanın akış hızının gözlemcinin mekansal hızına göreli olduğu sonucuna varıyor. Yani zamanın akış hızının mutlak olmadığını söylüyor.

Aslında bu kuramın çizdiği tabloda zaman ayaklarımızın altından akmıyor, biz onun üzerinde kayıyoruz. Kendi hareketimizi onun hareketi sanıyoruz ve mekanda hızlandıkça, onda yavaşlıyoruz.

Resim-1: Minkowski Uzayı

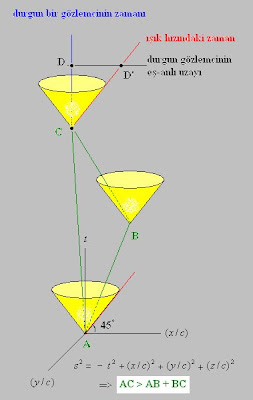
Resim-1 Özel Görelilik Kuramı'nın doğa kurgusunu temsil eden Minkowski Uzayı’nda yer değişiminin nasıl tanımlandığını gösteriyor. A, B ve C 4 boyutlu uzayda (/mekan-zamanda) gerçekleşen birer olayı gösteriyor. 4 boyutlu uzayı resmetmek zor olduğu için çizimlerde mekan boyutlarından biri ihmal edilmiş durumda.

3 boyutlu uzayda bir olaydan sonra saçılan ışık parçacıklarının mekan-zaman yol izleri bir koni yüzeyi tanımlıyor ve olayda oluşan herhangi bir şeyin zamansal yol izi bu koninin dışına çıkamıyor [1]. Bu temsilde sabit mekansal hızdaki gözlemcilerin zamansal yol izlerine doğrular, ivmeli mekansal hızdaki gözlemcilerin zamansal yol izlerine ise eğriler karşılık geliyor.

Resimdeki A noktasında iki ikiz kardeşten birinin ışık hızına yakın bir mekansal hızda bir uzay aracına bindiği düşünülsün. Bu kardeş uzay aracıyla önce bir gezegene gitsin (B noktası), sonra da dünyaya geri dönüp, ikiziyle buluşsun (C noktası). Bu bakışımsız (/anti-simetrik) örnekte C noktasındaki buluşmada ikizlerden yolculuk yapanının diğerine göre daha az yaşlanmış olması gerekiyor. Çünkü onun gittiği zamansal yol (vektör boyu için verilen denklem kullanılarak gösterilebilen) üçgen eşitsizliğine göre kardeşininkinden daha kısa [2].

Kuramda uzaydaki bir noktada bulunan bir gözlemcinin eş-anlı uzayı (/şimdisi) doğal olarak onun mekansal hızıyla ilintili oluyor (Resim-2). Yani yanyana olan iki mekan-zaman noktasında bulunan ama mekansal hızları farklı olan iki gözlemcinin eş-anlı uzayları da farklı olabiliyor ve böylece aynı anda olma durumu öznelleşiyor.

Resim-2: Eş-anlı Uzaylar

Şimdinin mutlaklığının yitişi daha derinlemesine bakılınca zamanın akış yönünün mutlak olmayışını doğuruyor: Bir gözlemciye göre bir A olayı geçmişte, bir B olayı gelecekteyken; bir diğer gözlemciye göre aynı B olayı, aynı A olayından önce olabiliyor! (Resim-3)

Resim-3: Geçmiş ve Gelecek

Genel Görelilik Kuramı'nda ise kütle çekimi alanındaki bir hareketin ivmeli hareket etmekle temelde özdeş olduğu anlaşılıyor. Madde (/kütle) ve mekan-zamanın etkileştiği, madde-madde etkileşimlerinin bunun bir türevi olduğu gösteriliyor. Maddenin mekan-zamanı bükmesi sonucunda yukarıdaki resimlerde zamansal yol izlerini temsil eden doğrular eğrilerle yer değiştiriyor.

Resim-4: Madde ile Mekan-Zaman Etkileşimi

Boş uzayda iki eş uzunlukta olan zamansal yollardan (Resim-4, [AB] ve [A'B’] doğruları) birisi daha yoğun bir kütleçekim alanından geçiyorsa, daha çok eğriliyor ve böylece boyu kısalıyor. Bu yüzden o zamansal yolu giden bir gözlemci, aynı mekansal hızda ama diğer zamansal yolu giden bir gözlemciden az yaşlanmış oluyor.

Resim-5: Karadelikler

Kütleçekim alan yoğunluğu belirli bir eşik değerden yüksek olan kaynaklardan ışık hızındaki bir gözlemci bile kaçamıyor. Karadelik olarak adlandırılan böyle bir kaynağın olay ufkunda (/yakın komşuluğunda) yörüngeye giren sabit mekansal hızdaki bir gözlemci için (Resim-5 A) gidilebilecek toplam zamansal yol belirli bir sürede sabitleniyor. Çünkü temsildeki zamansal yol-izi kapalı bir eğri oluşturuyor.

Resim-5 A'daki yörüngenin yarıçapı (r) sıfıra giderken gözlemcinin gittiği zamansal yol (-2пr), yani zamansal hızı sıfıra gidiyor. Böylece zaman gözlemci için nerdeyse duruyor. Yarıçap sonsuza giderken ise gözlemcinin zamansal hızı sonsuza gidiyor ve onun için zaman sonsuz hızda akıyor. Makul bir yarıçapta ise belirli süre geçtikten sonra gözlemci yörüngeye girdiği ilk ana geri dönmüş oluyor ve her şey yeniden yaşanmaya başlıyor. Ve bu kısır döngü içrek ya da dışrak bir müdahale olmadığı sürece devam edip, duruyor.

Karadeliğin üzerine düşen bir gözlemcinin (Resim-5 B) düşüş sırasındaki algılayabildiği toplam zamansa düşüşün başladığı yükseklik arttıkça azalıyor. Karadeliğin içine girdikten sonrası ise büyük bir giz..

Günlük yaşantıda yüksek hızlarda mekanda hareket edilmediği ve neredeyse tekdüze bir kütleçekim alanı içinde bulunulduğu için zamanın akış hızı ve yönünde anlamlı değişimler gerçekleşmiyor. Fakat gezegenlerin yörüngeleri gibi birçok olgu sadece mekan-zamanı bir kabul eden görelilik denklemlerince tam olarak anlamlı hale geliyor. Böylece Görelilik Kuramı alışıldık olanı kapsayacak ama farklı bir fiziksel gerçeklik anlayışı gerektirmiş oluyor.

* * *

0) Sabit bir hızda hareket eden bir gözlemcinin kendisini merkezinde durgun kabul ettiği koordinat sistemi, onun eylemsiz (/ivmesiz) referans sistemi olarak adlandırılıyor.

1) Minkowski Uzayı gerçel bir vektör uzayıdır. Bu uzayda boyu pozitif olan vektörler mekansal vektörler, boyu negatif olan vektörlerse zamansal vektörler olarak adlandırılıyor. Yani t ekseniyle yaptığı açı 45 dereceden küçük olan ve böylece koninin içinde kalan doğrular zamansal yol izlerine karşılık geliyor. Zamansal ve mekansal vektörleri ayıran ve koni yuzeyi oluşturan vektörler ise ışık hızındaki birinin hem zamansal, hem de mekansal yol izi oluyor.

Açık bir şekilde r/c = 0 doğrusu (mavi doğru) mekansal hızı sıfır olan bir gözlemcinin zamansal yol izini gösteriyor. 3 boyutlu Minkowski Uzayı’nda mekansal hızı sıfır olan gözlemci için vektör boyu s^2 başlangıç anından sonra hep negatif bir değerde oluyor:

s^2 = - t^2 + (x/c)^2 + (y/c)^2 = - t^2 + (r/c)^2
= - t^2 + ((0t/c))^2 = - t^2 + 0 = - t^2 < 0

Mekansal hız arttıkça (r/c)^2 terimi arttığı için yukarıdaki uzunluk sürekli artıyor. Minkowski Uzayı'nda mekansal hızı ışık hızı c olan bir gözlemci için olan vektör boyu ise sıfır bulunuyor:

s^2 = - t^2 + (x/c)^2 + (y/c)^2 = - t^2 + (r/c)^2
= - t^2 + ((ct/c))^2 = - t^2 + t^2 = 0

Mekansal hızın c'yi geçmesi ise uzunluğu pozitif yapıyor ve bu durumda zamansal yol izi tanımlanamıyor.

2) Bakışımı kıran şey yolculuk yapan kardeşin eylemsiz bir referans çerçevesinde bulunmaması oluyor. Eğer bakışım kırılmasaydı, yolculuk yapan kardeşin eylemsiz referans çerçevesinden dünyada onu bekleyen ikizi onun hızıyla hareket ediyor gibi görünürdü. Bu bakış açısından dünyadaki kardeşin daha az yaşlanmış olması gerekirdi. Sonuç olarak da bir paradoks oluşurdu.