Düzensizliği Ölçmek – II: Bağlamsallık

 Bu yazı dizisine başlarken bir sistemin ne kadar düzensiz olduğunu anlayabilmek için önce o sistemin fiziksel durumunu matematiksel olarak tarif etmek gerektiğini söylemiş ve bunu olasılık dağılımları kullanarak nasıl yapabileceğimizi göstermeyi denemiştik [1]. Dizinin ikinci yazısında ise entropi ve majorizasyon gibi bazı düzensizlik ölçütlerinin tanıtılacağının haberini vermiştik. Affınıza sığınarak bu tanıtımı şimdilik üçüncü yazıya ertelemek ve onun yerine düzensizlik ve olasılık dağılımları üzerinde biraz daha durmak istiyoruz.

  Şekil 1: 60 özdeş kırmızı noktanın aynı alan içindeki olası 3 farklı dağılımı (A,B,C) ve örnek bir düzen(sizlik) bağlamı olarak 45 özdeş dikdörtgenden oluşan bir ızgara (D) [2].

Sizce Şekil 1’de A, B ve C olarak adlandırılan 3 farklı dağılımdan en düzenli ve en düzensiz olanları hangileri? İlk bakışta en düzenli dağılım A olarak görünüyor, değil mi? Peki en düzensiz dağılım B mi, C mi? Karar verebildiniz mi? Elimizde bu 60 özdeş noktadan oluşan sistem hakkında daha fazla bilgi olmadan aslında bu 3 uzamsal dağılımdan herhangi birinin diğerinden daha düzenli/düzensiz olduğunu söyleyemeyiz. Sistemin durumunu bir olasılık dağılımı ile tarif edebilmek için bir bağlama ihtiyacımız var. Şekil 1’de D ile gösterilen özdeş dikdörtgenlerden oluşan ızgara bu anlamda bir bağlam olarak kullanılabilir. Rastgele seçilen bir noktanın

• herhangi bir dikdörtgenin köşesinde olma olasılığı pV,
• herhangi bir dikdörtgenin kenarında olma olasılığı pE,
• herhangi bir dikdörtgenin içinde olma olasılığı pI,
• hiçbir dikdörtgenin içinde olmama olasılığı pO

olsun (*). Noktaların herhangi bir uzamsal dağılımını bunun ardından şu şekilde tarif edebiliriz:

p(X) = (pV, pE, pI, pO) .

Buna göre A olarak adlandırılan olasılık dağılımı azami düzene (ya da eşdeğer ifadeyle asgari düzensizliğe) karşılık gelir (Şekil 2):

p(A) = (60/60, 0/60, 0/60, 0/60) = (1, 0, 0, 0) .

B ve C’nin olasılık dağılımları ise Şekil 2’deki kırmızı, turuncu, yeşil ve mavi noktalar teker teker sayılarak şu şekilde bulunur:

p(B) = (0/60, 12/60, 40/60, 8/60) ,

p(C) = (2/60, 10/60, 30/60, 18/60) .

Şekil 2: Şekil 1’deki A,B ve C uzamsal dağılımlarının 45 özdeş dikdörtgenden oluşan D ızgarası üzerine yerleştirilmiş hali [2]. Olasılık hesaplarını kolaylaştırmak için herhangi bir dikdörtgenin köşesinde olan noktalar kırmızı, herhangi bir dikdörtgenin kenarında olan noktalar turuncu, herhangi bir dikdörtgenin içinde olan noktalar yeşil, bunların dışındaki noktalar ise mavi renkle gösterildi.

Bir sonraki yazıda göreceğiz ki p(A), p(B) ve p(C) olasılık dağılımlarının tarif ettikleri düzensizlik miktarları entropi cinsinden sırasıyla 0, 1.24 ve 1.62 olacak (**). Yani en düzenli dağılım A iken, en düzensiz dağılım C bulunacak. Fakat Şekil 1’deki D bağlamından başka bir bağlama geçtiğimizde bu sıralama baştan sona değişebilir.

Şekil 3: Ünlü besteci Ludwig van Beethoven'in “Für Elise” adlı bestesinin [3] açılış notaları üzerine Şekil 1’deki B dağılımı yerleştirilmiş hali [2].

Şekil 3’de görüldüğü gibi B dağılımı D ızgarası yerine boş bir porte kağıdına yerleştirildiğinde ortaya 1810 yılında bestelenip, 1867 yılında yayınlanan ve o zamandan beri dünyanın en bilindik müziklerinden birisi olan Für Elise’nin açılışı çıkıyor. Benzer bir şekilde C dağılımı 1945 yılında Picasso’nun yaptığı meşhur boğa soyutlaması Le Taureau’nın altıncı tasvirinin kaba hatlarını veriyor (Şekil 4).

Şekil 4: Ünlü ressam Pablo Picasso'nun “Le Taureau” adlı taş baskısının [4] altıncı aşaması üzerine Şekil 1’deki C dağılımı yerleştirilmiş hali [2].

A uzamsal dağılımı D ızgarası bağlamında gösterdiği azami düzen özelliğini Beethoven’in notaları bağlamında B dağılımına, Picasso’nun çizgileri bağlamında ise C dağılımına bırakacak.

D ızgarasının Für Elise’den ya da Le Taureau’dan daha yüksek bir düzen ifade ettiğini söyleyemeyiz. Bu yüzden A, B ve C gibi ilk bakışta düzensizlikleri karşılaştırılabilir görünen farklı durumları bağlamdan bağımsız bir şekilde ele alamayız. Bağlam olmadan olasılıklar, olasılıklar olmadan da düzensizlik tanımlanamaz.

Bilimle kalın efendim,

Yazar: Onur Pusuluk
Editörler: Burcu Erdoğan, Güney Akbalık, Bilge San

(*) pV, pE, pI ve pO’da olduğu gibi olasılık çoğu zaman İngilizce karşılığı olan “probability” kelimesinin baş harfine gönderme yaparak “p” ile gösterilir. Bir de yeri gelmişken hatırlatalım, olasılık her zaman 0 ve 1 arasında bir sayı olmalı. Toplam olasılıksa korunmalı: pV + pE + pI + pO = 1.
(**) Bu yazı dizisindeki bir sonraki yazının başlığının Düzensizliği ölçmek – III: Entropi olması planlanıyor.

Kaynakça:  

[1] “Düzensizliği Ölçmek – I: Olasılık Dağılımları” başlıklı bu yazıya aşağıdaki bağlantıdan ulaşabilirsiniz:

https://epistemturkiye.org/duzensizligi-olcmek-i-olasilik-dagilimlari/ 

[2] Görsek kaynaklar: Onur Pusuluk.

[3] Parçanın piyano versiyonunu buradan dinleyebilirsiniz:

https://www.youtube.com/watch?v=_mVW8tgGY_w 

[4] Çizimin tüm aşamalarına buradan bakabilirsiniz:

http://mourlot.free.fr/english/fmtaureau.html

Yazının epiSTEM Türkiye bağlantısı:

https://epistemturkiye.org/duzensizligi-olcmek-ii-baglamsallik/

Düzensizliği Ölçmek – I: Olasılık Dağılımları - epiSTEM Türkiye

Canlıların ortak özellikleri arasına cansız çevreleriyle karşılaştırıldıklarında gösterdikleri ileri düzeydeki atomik, moleküler ve hücresel düzeni de ekleyebiliriz. Fakat fizik kanunları canlılar ve cansızlar arasında hiçbir ayrım yapmaz. Bu bağlamda termodinamiğin ikinci yasasını özellikle anmak gerekiyor. Toplam düzensizliğin her zaman artacağını öngören bu yasanın hüküm sürdüğü bir ortamda düzeni korumak hiç de kolay değildir: moleküller dağılıp yıkılma, hücreler ise yaşlanıp ölme eğilimindedir ve canlılar hayatta kalmak için onların yerine yenilerini koymak zorundadırlar. Bunun için de enerji harcamalı ve kendi içlerinde yeniden kurdukları düzenden daha yüksek oranda bir düzensizliği çevrelerinde yaratmalıdırlar. 

Düşünsenize, şu an akciğerlerinizden beyninize oksijen taşıyan kırmızı kan hücreleriniz en fazla iki ay hayatta kalabiliyor. Neyse ki aldığınız besinleri parçalayarak elde ettiğiniz enerji ve düzensizlik onlar öldüğünde yerlerine yenilerinin çoktan üretilmiş olması için yeterli. Fakat beyninizdeki sinir hücreleri (bildiğimiz kadarıyla) çoğalma özelliğine sahip değil. Bu yüzden siz hayatta kaldıkça onlar da canlılıklarını korumalı. Üstelik zihinsel yeteneklerinizi kaybetmemek için bu da yeterli değil. Sinir hücrelerinizin bir araya gelerek oluşturduğu karmaşık hücresel düzen de yerli yerinde olmalı. Tabii çevreden daha çok enerji alarak ve çevrede daha çok düzensizlik yaratarak... 

Canlı bir organizma çevresiyle arasındaki düzen/düzensizlik dengesizliğini sonsuza kadar sürdüremez. Hem de çevresini genişletse ya da değiştirse bile! Termodinamiğin temel varsayımı olan “moleküler kaos”un [Not 1] kendi içine sızmasına artık karşı koyamadığı noktadan sonra hızla çevresiyle dengeye ulaşır: atom ve molekülleri arasında hiçbir ilinti kalmaz ve termodinamiğin ikinci yasasıyla uyumlu olarak yaşamını yitirmiş olur. 

Anlayacağınız, düzensizliği ölçmek – en azından bir bilim insanı için – bir ölüm kalım meselesi kadar önemli olabilir. Fakat bu sizi yazının devamını okumaya ikna etmediyse, lütfen önce Not 2’ye bir göz atın. 

Moleküler ve atomik düzensizliklerin matematiksel temsili 

Bir sistemdeki düzensizliği ölçebilmek için önce o sistemin fiziksel durumunu matematiksel olarak tarif edebilmemiz gerekiyor. Bunun için en sık kullanılan araçlardan bir tanesi “olasılık dağılımı”. Bu yazının geri kalan kısmını sadece buna ayıracağız: tasviri canlı sistemlerden daha basit, ama yaşam için önemi tartışılmaz olan su molekülünü (H₂O) örnek göstererek, düzensizlikten olasılıksal olarak ne kastettiğimizi ve düzensizliği ne pahasına azaltabileceğimizi anla(t)mayı deneyeceğiz.

Gelin ilk olarak suyun moleküler yapısına biraz yakından bakalım. Bir su molekülü, kovalent bağ olarak adlandırılan kuvvetli kimyasal bağlar aracılığıyla iki tane hidrojen (H) atomu ile bir tane oksijen (O) atomunun bir araya gelmesinden oluşur. Hidrojen ve oksijen atomlarının sırasıyla beyaz ve kırmızı küreler, kovalent bağların ise birer küçük siyah çubuk ile temsil edildiği Şekil 1'de 15 tane su molekülünden oluşmuş bir moleküler öbeğin tasvirini bulabilirsiniz. Gördüğünüz gibi, bu tasvirde su molekülleri arasında yer yer mavi kesikli çizgilerle resmedilmiş bazı etkileşimler var. Bu etkileşimler aslında hidrojen bağı adı verilen ve kovalent bağlardan görece daha zayıf olan kimyasal bağlar.

Şekil 1: Sıvı haldeki su molekülleri. Kırmızı küreler oksijen (O), beyaz kürelerse hidrojen (H) atomlarını gösteriyor. Farklı H₂O moleküllerine ait oksijen ve hidrojen atomlarını birbirine bağlayan koyu mavi kesikli çizgiler hidrojen bağlarını temsil ediyor. 

Tek bir su molekülü aynı anda en fazla 4 farklı su molekülü ile hidrojen bağı kurabilir. Fakat moleküllerin 0 °C’nin üzerindeki sıcaklıklarda sahip oldukları hareket enerjisi çoğu zaman bu bağların kırılması için yeterlidir. Bu sıcaklıklarda suyun katı değil de akışkan olması da aslında molekülleri arasındaki hidrojen bağlarının rahat bir şekilde kırılıp yeniden kurulabilmesi sayesindedir.

Bir su molekülü en fazla 4, en az 0 hidrojen bağı kurabileceği için, kendisine baktığımız bir anda görebileceğimiz 5 farklı durum var: etrafındaki diğer moleküller ile arasında

- hiç hidrojen bağı olmayabilir,
- sadece 1 hidrojen bağı olabilir,
 - 2 hidrojen bağı olabilir,
- 3 hidrojen bağı olabilir,
- 4 hidrojen bağı olabilir.

Bu bağlamda, sabit bir T sıcaklığındaki suyun moleküler düzensizliğini, kabaca da olsa, rastgele seçtiğimiz bir su molekülünün sahip olacağı hidrojen bağı sayısının olasılık dağılımı “p” ile şu şekilde tarif edebiliriz [Not 3] :

p(T) = (p4, p3, p2, p1, p0) ,

Öyle ki, seçtiğimiz su molekülü p4 olasılığıyla 4, p3 olasılığıyla 3, p2 olasılığıyla 2, p1 olasılığıyla 1, p0 olasılığıyla 0 hidrojen bağına sahip olsun. Buna göre azami düzensizliğe karşılık gelen olasılık dağılımı şöyledir:

p(T_max) = (1/5, 1/5, 1/5, 1/5, 1/5) .

Bu durumda her su molekülü ortalama 2 hidrojen bağına sahip olur: (4+3+2+1+0)/5 = 2. Oda sıcaklığı gibi daha düşük sıcaklıklarda, 20–25 °C arasında, bu sayı 3.4’e çıkar [Not 4]. Ortalama 3.4 hidrojen bağını mesela

p(T_oda; 1) = (3/5, 1/5, 1/5, 0, 0)

ya da p(T_oda; 2) = (2/5, 3/5, 0, 0, 0)

gibi bir dağılımdan elde edebiliriz. Bu her iki dağılım da p(T_oda)’tan daha az düzensiz birer durumu tarif eder: genel olarak hidrojen bağı sayısıyla ilgili rastgelelik azalmış ve tahmin edilebilirlik artmıştır. Su T = 0 °C sıcaklığına soğutulduğunda ise sıvı halden katı hale geçişin bir göstergesi olarak moleküler düzensizlik yerini Şekil 2'de kısmen betimlenen ve aslında her molekülün 4 tane hidrojen bağı yaptığı azami düzene bırakır:

p(T_buz) = (1, 0, 0, 0, 0) .

Şekil 2: Hekzagonal su buzundaki bir birim hücrenin sadece bir yüzeyinde bulunan 6 su molekülü. Moleküler yapının tamamını her bir yüzeyin sandal ya da sandalye şeklinde katlanarak birbirine bağlandığı üç boyutlu bir kristal olarak hayal edebilirsiniz. Bu üç boyutlu yapıda her bir su molekülü 4 farklı su molekülü ile hidrojen bağı yapacaktır. 

Bu noktadan sonra bütün oksijen atomlarının mevcut konumlarında donduğunu düşünebilirsiniz. Fakat onlardan çok daha küçük bir kütlesi olan hidrojen atomları çok düşük sıcaklıklara kadar bir molekülden diğerine hidrojen bağları üzerinden hoplayabilir. Bu yüzden su buzunun içinden rastgele seçilen bir su molekülü Şekil 3'te gösterilen 6 farklı bağlanma durumundan herhangi birinde bulunabilir. Yani moleküler ölçekten atomik ölçeğe geçtiğimizde başka bir düzensizlik seviyesi ile karşılaşırız.

Bu atomik düzensizliği de, öncekine benzer bir yol izleyerek, rastgele seçilen bir molekülün Şekil 3'teki durumlarda olma olasılığının dağılımı “q” ile tarif edebiliriz:

q(T) = (q1, q2, q3, q4, q5, q6)

T = 0 °C sıcaklığında molekülün her bir durumda bulunma olasılığı birbirine eşit olduğu için atomik düzensizlik azamidir:

q(0 °C) = (1/6, 1/6, 1/6, 1/6, 1/6, 1/6) .

Sıcaklık daha düşük değerlere indikçe atomik düzensizlik de azalır. Öyle ki, –200 °C’nin biraz altında bütün moleküller olası durumların sadece bir tanesinde, mesela birincisinde [Not 5], bulunurlar:

q(-200 °C) = (1, 0, 0, 0, 0, 0) .

 Şekil 3: 4 tane hidrojen bağı (mavi kesikli çizgiler) yapan bir su molekülünün olası bağlanma durumları. Sadelik adına bu merkezi molekülün dışındaki diğer su moleküllerinin bütün hidrojen atomları (beyaz küreler) resme dâhil edilmemiştir. 

Böylece aşırı soğutulan su molekülleri arasında moleküler düzenin ardından, atomik düzene de ulaşılmış olur. Buzdolabınız bu kadar büyük miktarda enerji harcasaydı elektrik faturanız ne kadar yüksek olurdu, düşünsenize. Tahmin edebileceğiniz gibi suda bu şekilde bir düzen yaratmanın maliyeti oldukça yüksek. Fakat canlı hücreler içlerindeki küçük su öbekleri üzerinde, üstelik de vücut sıcaklığında, bahsi geçen atomik ve/veya moleküler düzenleri gerçekleştirebiliyor [Not 6] Sonra da su molekülleri arasındaki düzeni bozup, oluşan düzensizliğin gölgesinde kendi içinde başka bir atomik ve/veya moleküler düzen kurabiliyor.

Daha fazla matematik 

Bir sonraki epiSTEM yazımda size entropi ve majorizasyon gibi bazı düzensizlik ölçütlerini tanıtmayı planlıyorum [Not 7]. Onun ardından burada anlatılan düzensizliğin olasılık dağılımı ile tarifi de ete kemiğe bürünmüş olacak. Göreceğiz ki p(T_max), p(T_oda; 1) ve p(T_oda; 2) olasılık dağılımlarının tarif ettikleri düzensizlik miktarları entropi cinsinden sırasıyla 2.32, 1.37 ve 0.97 olacak. Bu dağılımlar arasındaki majorizasyon ilişkilerini kullanarak da birbirleri arasındaki geçişlerin mümkün olup olmadığını inceleyeceğiz. Fakat şimdilik burada durup, biraz dinlenelim.

Bilimle kalın efendim,

Yazan: Onur Pusuluk
Düzelten: Özge Yoluk, Bilge San

Notlar: 

[1] Yazıda “moleküler kaos”tan kastedilenin ne olduğunu daha iyi anlamak için aşağıdaki bağlantıya, özellikle de orada verilen son paragrafa bakabilirsiniz:

https://en.wikipedia.org/wiki/Molecular_chaos

[2] Kabaca özetlemeyi denediğim, düzensizliğin bizleri bekleyen kaçınılmaz sonda oynadığı belirleyici rol, onu matematiksel olarak ölçmemiz gerektiği konusunda herkesi yeterince ikna etmemiş olabilir. Fakat sizi temin ederim ki termodinamiğin ikinci yasası sadece biyolojide hüküm sürmez: fizik ve kimyadan, makine ve haberleşme mühendisliğine, hatta ekonomiye kadar bildiğimiz her yerde geçerlidir. Bizler için önemli birçok hesap düzensizliğin ölçülmesini gerektirir. Benim aklıma ilk gelenler şunlar:

- mutfakta kullandığınız su ısıtıcısının, buzdolabının ya da her gün evden işe gitmek için bindiğiniz motorlu aracın azami enerji verimi,
- bilgisayarınızda sakladığınız dosyaların, internete yüklediğiniz videoların ve cep telefonunuzdan gönderdiğiniz mesajların azami ne kadar sıkıştırılabileceği,
- bir ülkenin gelir dağılımındaki eşitsizliğin ve buna dayanarak ülkelerin refah seviyelerinin karşılaştırılması.

Belki bir başka yazıda bunları da ele alabiliriz.

[3] Tabii bu sıcaklık 100 °C’nin altında bulunan belli bir üst limitten küçük olmalı. Çünkü moleküllerin (ısıl) hareket enerjilerinin aralarındaki hidrojen bağlarının enerjisinden çok daha büyük olduğu sıcaklıklarda düzensizliği hidrojen bağı sayısı üzerinden tanımlayamayız. Unutmayın ki su 100 °C’ye ısıtıldığında bütün hidrojen bağları kırılacağı için bir anlamda sıvı halden gaz hale geçilmiş olacak.

[4] Bu sayı neredeyse bütün biyokimya ve biyofizik kitaplarında suyun yapısı anlatılırken karşınıza çıkabilir. Fakat ilk kaynağın ne olduğunu maalesef şu anda ben de bilmiyorum.

[5] Moleküller –200 °C’nin altında tünelleme adı verilen bir kuantum mekaniksel olgu yüzünden Şekil 3’teki birinci durumdan bir diğerine, mesela ikinci duruma geçebilirler. Fakat bu, bir ölçüm yaptığımızda hepsinin aynı durumda bulunacağı gerçeğini değiştirmez. Dolayısıyla moleküllerin düzeni/düzensizliği değişmez.

[6] Canlı hücrelerin içinde bulunan “hapsedilmiş su” (“confined water”) bildiğimiz sıvı haldeki sudan birçok açıdan farklıdır ve bazen atomik ve moleküler düzen gibi su buzuna özgü olan bazı özellikleri gösterebilir. Aşağıdaki iki bağlantıdan sırasıyla hücrenin içindeki su ve (genel olarak) hapsedilmiş su ile ilgili daha fazla bilgi bulabilirsiniz:

http://www1.lsbu.ac.uk/water/intracellular_water.html

http://www1.lsbu.ac.uk/water/confined_water.html

[7] Bu yazı dizisinde ikinci yazının başlığının Düzensizliği ölçmek – II: Entropi, Majorizasyon ve Lorenz Eğrisi olması planlanıyor.


Yazının epiSTEM Türkiye bağlantısı:

https://epistemturkiye.org/duzensizligi-olcmek-i-olasilik-dagilimlari/

Suyun Kuantum Fiziği? - epiSTEM Türkiye

Hem yerel, hem de küresel medya maalesef uzun bir süredir suyun hafızasının kuantum mekaniksel temelleri üzerine kurulu sözde-bilimsel mistik öğretilerin bombardımanı altında kalmış durumda. Böyle bir ortamda toplumun zihinsel hijyenini korumak hiç de kolay değil. Fakat bu uğurda akademik çevrelerde çok şey yapıldığı da söylenemez. Bu yazı biraz da bu eksiklik karşısındaki mahcubiyetle kaleme alınmıştır. 

Suda kuantum mekaniksel olgular gerçekleşiyor olabilir mi? 

Diğer sıvılarla karşılaştırıldığında suyun gerçekten de kuraldışı ya da tuhaf olarak adlandırılabilecek birçok yapısal, dinamik ve termodinamik özelliği var [1]. Fakat bu özelliklerin çoğu sadece suyu oluşturan H₂O moleküllerinin arasındaki klasik etkileşimler ele alınarak açıklanabilir [2]. Tabii klasik hesapların başarısı kuantum fiziğinin oyuna dâhil olmadığı anlamına gelmez. Zira birbirine zıt yönde etkileri olan bazı kuantum mekaniksel olgular söz konusu olabilir [3]. Ya da klasik hesaplarda kullanılan bazı yaklaşımlar hesaba katılmayan kuantum etkilerini taklit ediyor olabilir [4].

Not-1’de ayrıntılarını bulabileceğiniz suda ortaya çıkabilecek olan kuantum mekaniksel olgular, suyun kendisini oluşturan H₂O moleküllerindeki hidrojen (H) atomlarının ya da bu atomların çekirdeklerindeki protonların hareketinden kaynaklanır. Zaten bir hidrojenin çekirdeği sadece bir protondan oluşur. Onun bir izotopu olan ve “ağır hidrojen” olarak da bilinen döteryumun (D) çekirdeğindeyse bir proton ve bir nötron birlikte bulunur.

Suyun içindeki hidrojen atomları deneysel olarak döteryum atomlarıyla değiştirilebilir. Bu da hidrojen atomlarının ya da bu atomların çekirdeklerindeki protonların hareketine bağlı olarak suda ortaya çıkabilecek olan, doğaları gereği kütle ile ters orantı içindeki kuantum mekaniksel olguların etkilerini azaltır. Bu bağlamda, H₂O moleküllerinden oluşan “hafif su” üzerindeki deneysel ölçümlerde görülen bir tuhaflık eğer D₂O moleküllerinden oluşan “ağır su” üzerindeki deneysel ölçümlerde ortadan kayboluyorsa, bu tuhaflığın aşikâr olmayan bazı kuantum etkilerinden kaynaklandığı iddia edilebilir. Yani dolaylı da olsa bu konudaki varsayımları test edebilecek deneysel yöntemler literatürde mevcut.

Peki, suda hidrojen/proton hareketine bağlı kuantum mekaniksel olgular ne zaman ortaya çıkar?

Öncelikle (hidrojen bağı ile) etkileşen iki su molekülünün oksijen (O) atomları arasındaki uzaklık santimetrenin yüz milyonda birinin 2.6 katından – yani 2.6 Angstrom’dan – küçük olmalı. Ayrıca aralarındaki hidrojene/protona bu iki oksijen atomunun ilgileri – hidrojene/protona kovalent olarak bağlandıkları zaman saldıkları enerjiler – arasındaki fark kabaca 20 kcal/mol’dan az olmalı. Son olarak, hidrojen/proton bu iki oksijen atomunu birbirine bağlayan hayali doğruya mümkün olduğunca yakın bulunmalı. Daha doğru bir ifadeyle, su molekülleri arasında doğrusala yakın bir bağ kurulmalı.

Bildiğimiz suda oksijen atomları arasındaki uzaklık ortalama 2.8 Angstrom kadardır. Bu atomların proton ilgileri arasındaki fark ise 20 kcal/mol mertebesindedir. Isıl salınımlar sebebiyle yer yer bu değerlerde keskin düşüşler gerçekleşebilir. Fakat aynı salınımlar su molekülleri arasında yeterince uzun süre doğrusal bir bağ kurulmasına izin vermez. Bu da demektir ki gündelik algılarımızla çelişkili görünen kuantum mekaniksel olguların (bkz Not-1) bildiğimiz suyun yapısal, dinamik ve termodinamik özellikleri üzerinde önemli bir etkisinin olması çok beklendik bir şey değildir.

Suyun bazı katı hallerinde/fazlarında ise durum oldukça farklı. Yanlış okumadınız, su buzunun onlarca farklı hali/fazı mevcut. Üstelik bunların bazılarında belli sıcaklık ve basınç değerleri aralıklarında kuantum tünelleme (bkz Not-1-b) gibi olguların gerçekleştiğine dair birçok kuramsal, hesapsal ve deneysel çalışma yapılmış [5].

Metrenin milyarda biri ölçeğinde sentezlenmiş karbon nano-tüplerde ya da canlı hücrelerin içinde bulunan “hapsedilmiş su” da bu bağlamda su buzunun bazı halleri/fazları gibi bildiğimiz sudan ayrı tutulabilir. Fakat şu an konumuz şu fani hayatlarımızda daha az gördüğümüz suyun bu farklı yüzleriyle ilgili değil.

 Figür 1: H₂O moleküllerinden oluşan su öbeklerinin dinamiği. Kırmızı küreler oksijen (O) atomlarını, beyaz küreler hidrojen (H) atomlarını, yeşil çizgilerse hidrojen bağlarını temsil ediyor.

Kaynak: http://www1.lsbu.ac.uk/water/water_equilibria.html 

Suyun hafızası olabilir mi? 

Su, daha önce içerisinde çözülmüş olan bir maddeyi hatırlayabilir mi? Hatta bu hatıra üzerinden o maddenin şeklini, dolayısıyla da biyokimyasal etkinliğini taklit edebilir mi?

Suyun (içinde çözülmüş olan antikorlar için) böyle bir hafızasının olduğu 1988 yılında Fransız immünolog Jacques Benveniste önderliğinde yapılan ve dünya çapında dört farklı bağımsız araştırma merkezinde tekrarlanan, sonuçları oldukça tartışmalı bir deneyin sonunda iddia edildi [6]. Hemen aynı yıl, Nature dergisinde bu deneyin sonuçlarının yayınlanmasına onay veren dergi editörü Sir John Royden Maddox önderliğindeki bir grup Benveniste’nin laboratuvarında kendilerinin kontrolünde yapılan tekrarlarda aynı sonuçları elde edemediklerini açıkladı [7]. Hâlâ da bu sonuçların doğruluğu/yanlışlığı üzerindeki tartışma tam olarak tatlıya bağlanmış durumda değil [8]. Fakat Benveniste’nin akademik saygınlığı bu tatsız tartışma sırasında zarar gördü ve ortaya attığı iddia bilim insanlarından daha çok bir alternatif tıp yöntemi olan homeopati [9] destekçileri arasında yankı buldu.

2009 yılından itibaren yayınlamaya başlayan bir dizi yeni deney sonucuna göre benzer bir iddia bu sefer DNA çözeltileri için ortaya atıldı [10]. Bu deneylerin başında HIV virüsünün keşfinde yer alan ve bu yüzden 2008’de fizyoloji ve tıp alanında Nobel bilim ödülüne layık görülen Fransız virolog Luc Antoine Montagnier vardı. Montagnier ve arkadaşları suyun daha önce içinde bulunan DNA molekülünü hatırlamakla kalmadığını, bununla ilgili bir elektromanyetik dalga yaydığını ve bu dalganın DNA’nın hatırasını başka bir kaptaki suya aktarabildiğini de öne sürdü. Fakat bu deneyler maalesef henüz başka bir bağımsız grup tarafından tekrarlanıp, doğrulanmış durumda değil. Ayrıca, Montagnier her ne kadar buna katılmasa da sonuçları alternatif tıp camiasına göre homeopati yönteminin [9] en önemli bilimsel destekleri arasına girdi.

Peki, bu deneysel sonuçları nasıl yorumlamamız gerekiyor? Gerçekten de suyun moleküler organizasyonun daha önce içinde bulunan maddeye göre şekil almasını fiziksel ve kimyasal bir tabana oturtturabilir miyiz?

Emin olun böyle bir bilimsel tabanın bulunması durumunda benden daha fazla heyecanlanacak bir fizikçi bulamazdınız. Daha dakikasında onlarca yeni kuramsal biyoloji modeli kurmaya başlardım. Fakat bildiğimiz fizik ve kimyaya göre bildiğimiz suda moleküler organizasyonun bu şekilde korunması mümkün görünmüyor. Her şeyden önce, su moleküllerini birbirine bağlayan hidrojen bağlarının ömrü saniyenin trilyonda biri – yani pikosaniye – mertebesinde bir zaman ölçeğinde.

Sudaki H₂O molekülü öbeklerinin ömrü hidrojen bağlarının ömründen uzun olamaz mı? Tabii ki olabilir. Fakat suda herhangi bir H₂O molekülü öbeği bir milisaniyeden daha uzun süre yapısal bütünlüğünü koruyamıyor (Figür 1). Oysa Montagnier ve arkadaşları suyun hafızasının haftalar boyunca sürdüğünü iddia ediyor.

Peki, suyun hafızası suyu oluşturan maddi gerçeklikten, hidrojen bağlı H₂O moleküllerinin toplamından daha aşkın bir şey olamaz mı? Yazının girişinde bahsi geçen sözde-bilimsel mistik öğretilerin iddiası suyun kuantum özellikleri sayesinde bunun tam olarak böyle olduğu yönünde. Fakat hafıza konusuna geçmeden önce gösterdiğimiz sebepler yüzünden kuantum mekaniksel olguların bildiğimiz suyun yapısal, dinamik ve termodinamik özellikleri üzerinde önemli bir etkisinin olması çok beklendik bir şey değil.

Son söz

Kuantum mekaniğinin doğuşunda yaşandığı gibi bazen bilimsel devrim niteliğinde sonuçları olan önemli araştırmalar akademik dünyada büyük bir sürtünme ile karşılaşabiliyor. Bazense çalıştığı alanda birçok devrim yapmış bir bilim insanı belli bir noktadan itibaren bilimin çizdiği ölçü ve çerçevenin dışına sürüklenip, hayatının geri kalanını kişisel inançlarının peşinde geçirebiliyor (bkz Not-2). Suyun hafızası ve bunun kuantum doğası gibi tartışmalı konularda durumun hangisi olduğunu anlamak çok da kolay değil aslında.

Anla(t)maya çalışırken bir hatamız olduysa affola.

Bilimle kalın,

Onur Pusuluk

Not-1:

Suda ortaya çıkabilecek olan başlıca kuantum mekaniksel olgular sıfır-noktası enerjisi, tünelleme, eş-evrelilik ve dolaşıklıktır. Meraklıları için birkaç cümle ile bunları açıklamak gerekirse:

a) sıfır-noktası enerjisi (zero-point energy): Bir kuantum mekaniksel sistemin mutlak sıfır sıcaklığı olan 0 Kelvin’de bile sahip olacağı titreşim enerjisi. Klasik fiziğe göre mutlak sıfır sıcaklığındaki herhangi bir atomun ya da molekülün donması, yani titreşim enerjisinin sıfır olması gerekiyor. Fakat Heissenberg belirsizlik ilkesi bağlamında bir kuantum mekaniksel sistemin sıfır-noktası enerjisi (her zaman içinde bulunduğu klasik potansiyel kuyusunun minimumundan büyük kalacak şekilde) salınım halinde olabiliyor.

Suda birbirine zıt yöndeki kuantum katkılar yüzünden hidrojenin/protonun sıfır-noktası enerjisinin klasik karşılığından çok farklı olması beklenmiyor [3].

b) tünelleme (quantum tunneling): Bir parçacığın klasik olarak aşamayacağı bir potansiyel engelini geçmesi. Kabaca duvara çarpan bir topun duvarın arkasına geçmesi olarak düşünülebilir. Fakat unutulmamalı ki bu olguyu gözlemlediğimiz fiziksel sistemler genellikle elektron ve proton gibi oldukça küçük parçacıklardan meydana gelir. Bu yüzden siz siz olun, sakın arkasına geçmek umuduyla bir duvara çarpmayın.

Özellikle su buzunun belli hallerinde/fazlarında protonların su molekülleri arasında tünellediği öne sürülüyor [5].

c) eş-evrelilik (quantum coherence): Kuantum üst üste binme (quantum superposition) ilkesine göre bir fiziksel sistem klasik olarak bulunabileceği birden fazla durumda aynı anda birden bulunabilir. Yukarıdaki açıklamada bahsi geçen topun aynı anda duvarın hem önünde, hem de arkasında bulunması gibi. Diğer bir ifadeyleyse, topun duvarın önünde ve arkasında bulunma durumları arasında eş-evrelilik olabilir.

d) dolaşıklık (quantum entanglement): Kuantum üst üste binmesi ilkesinin bir sonucu olarak iki farklı fiziksel sistem arasında yerel olmayan ilintiler ortaya çıkabilir. İki H₂O molekülü arasındaki hidrojen bağı boyunca protonun bir kuantum üst üste binme durumunda olması moleküller arasında böyle ilintiler üretebilir [5].

Not-2:

Benim kişisel hayranı olduğum, ikisi Nobel olmak üzere bir sürü ödül kazanmış olan Linus Pauling tam da böyle birisi sanırım. Daha fazla bilgi için: https://en.wikipedia.org/wiki/Linus_Pauling 

Kaynaklar:

[1] Daha fazla bilgi için: Anomalous properties of water @ Water Structure and Science: http://www1.lsbu.ac.uk/water/water_anomalies.html  

[2] Daha fazla bilgi için: J Russo et al, Water-like anomalies as a function of tetrahedrality, Proceedings of the National Academy of Sciences, 115 (15), E3333–E334 (2018). DOI: 10.1073/pnas.1722339115; Tetrahedrality is key to the uniqueness of water @ Phys.Org: https://phys.org/news/2018-03-tetrahedrality-key-uniqueness.html  

[3] Daha fazla bilgi için: S Habershon et al, Competing quantum effects in the dynamics of a flexible water model, The Journal of Chemical Physics, 131 (2), 024501 (2009). DOI: 10.1063/1.3167790 ; M Ceriotti et al, Nuclear Quantum Effects in Water and Aqueous Systems: Experiment, Theory, and Current Challenges, Chemical Reviews, 116, 7529–7550 (2016). DOI: 10.1021/acs.chemrev.5b00674  
[4] Daha fazla bilgi için: L Hernández de la Peña and Peter G. Kusalik, Temperature Dependence of Quantum Effects in Liquid Water, Journal of the American Chemical Society, 127 (14), 5246–5251 (2015). DOI: 10.1021/ja0424676  

[5] Daha fazla bilgi için: O Pusuluk et al, Emergence of correlated proton tunneling in water ice, arXiv/quant-ph (2018) @ https://arxiv.org/abs/1703.01335  

[6] E Davenas et al, Human basophil degranulation triggered by very dilute antiserum against IgE, Nature, 333, 816–818 (1988). DOI: 10.1038/333816a0  

[7] J Maddox et al, “High-dilution” experiments a delusion, Nature, 334, 287–290 (1988). DOI: 10.1038/334287a0

[8] Daha fazla bilgi için: S J Hirst et al, Human basophil degranulation is not triggered by very dilute antiserum against human IgE, Nature, 366, 525–527 (1993). DOI: 10.1038/366525a0 ; J Benveniste et al, Memory of water revisited, Nature, 370, 322 (1994). DOI: 10.1038/370322a0 ; Memory of water @ Water Structure and Science: http://www1.lsbu.ac.uk/water/memory_of_water.html  

[9] Daha fazla bilgi için: Homeopati nedir? : Tavşanın suyunun suyu @ Yalan Savar: https://yalansavar.org/2012/06/12/tavsanin-suyunun-suyu-1-homeopati-nedir/  

[10] L Montagnier et al, Electromagnetic signals are produced by aqueous nanostructures derived from bacterial DNA sequences, Interdisciplinary Sciences: Computational Life Sciences, 1, 81–90 (2009). DOI: 10.1007/s12539-009-0036-7 ; L Montagnier et al, Transduction of DNA information through water and electromagnetic waves, Electromagnetic Biology and Medicine, 34 (2), 106–112 (2015) . DOI: 10.3109/15368378.2015.1036072

Yazının epiSTEM Türkiye bağlantısı:

https://epistemturkiye.org/suyun-kuantum-fizigi/

Genetik Kod ve Moleküler Evrimi - epiSTEM Türkiye

Kalıtsal Bilginin Biyokimyasal Dili
 

Nükleik asitler canlılarda kalıtsal bilginin oluşturulması, depolanması, kodlanması ve değiştirilmesinden sorumlu olan polimerlerdir ve nükleotidlerin bir araya gelmesiyle oluşurlar.

Tek zincir bir nükleik asitte nükleotidler birbirine fosfat ve şeker grupları üzerinden kovalent olarak bağlı bulunur. Çok zincirli bir nükleik asitte zincirleri bir arada tutansa nükleotidlerin azotlu organik bazları – ya da kısaca nükleobazları -  arasındaki hidrojen bağlarıdır.

Doğada onlarca nükleobaz varken, nükleik asitlerin birbirleriyle konuşmak için kullandığı dilin alfabesi bunların sadece 5’ini harf olarak içerir: adenin (A), timin (T), guanin (G), sitozin (C) ve urasil (U). Burada konuşmadan kastedilen nükleobazlar arasında kurulan hidrojen bağları ile nükleik asitlerin birbiriyle etkileşmesi ve bu etkileşimler aracılığıyla kalıtsal bilginin bir molekülden diğerine aktarılması. 

Canlılar tarafından kalıtsal bilgiyi depolamak için kullanılan nükleik asitler deoksiribonükleik asit ve ribonükleik asittir, yani meşhur kısaltmalarıyla DNA ve RNA. DNA’da U, RNA’da ise T nükleobazı bulunmaz. Yani diğer nükleik asitlerle konuşurken bir DNA molekülü U harfini telaffuz edemez, bir RNA molekülü ise T harfini. Ve kalıtsal bilgi DNA’dan okunup RNA’ya ya da RNA’dan okunup DNA’ya yazılırken T ile U yer değiştirir. Böylece nükleik asitlerin alfabesi etkin olarak 4 harfe indirgenmiş olur.

DNA ya da RNA’da nükleobaz dizileri formunda taşınan toplam kalıtsal bilginin başka biyopolimerlerin sentezini kodlayan parçaları gen olarak adlandırılır. Bu polimerlerin başında taşıyıcı RNA (tRNA) ve ribozamal RNA (rRNA) gibi özel işlevleri olan bazı RNA çeşitleri ile amino asitlerin bir araya gelmesinden oluşan proteinler gelir. Bir hücrenin yaşamını devam ettirmek için ihtiyacı olan diğer tüm biyomoleküllerin sentezi de özünde birer protein olan, yani (birazdan kabaca özetleneceği şekilde) genlerdeki depolanan kalıtsal bilgiye göre sentezlenen enzimler tarafından katalize edilir.

Kalıtsal Bilginin Moleküler Akışı

DNA’nın çift zinciri (genellikle) Watson-Crick baz çiftleşmesi bağlamında birbirinin eşleniğidir, yani DNA’nın iki zincirinde A ile T, G ile de C karşı karşıya gelir [1]. Protein sentezinin ilk aşamasında (bazı enzimler aracılığıyla) öncelikle ilgili gen ve çevresinde bu nükleobazlar arasındaki hidrojen bağlarının kırılması ve zincirlerin birbirinden ayrılması gerekir. Bunun ardından (başka enzimler tarafından) zincirlerden biri kalıp olarak seçilir ve bu kalıptan yine Watson-Crick baz çiftleşmesi kullanılarak bir mesajcı RNA (mRNA) molekülü sentezlenir. 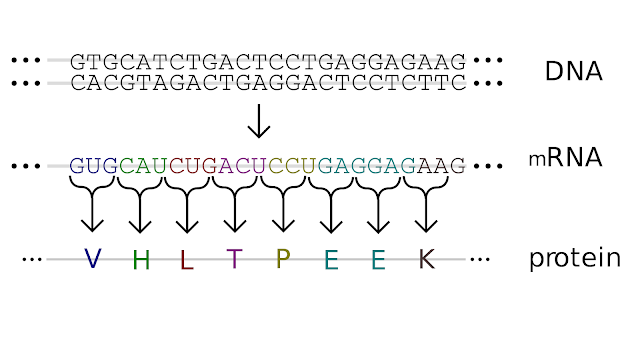Böylece kalıp zincirin eşleniğindeki kalıtsal bilgi Resim 1’in üst yarısında örneklendiği gibi mRNA’ya kopyalanmış olur.

İkinci aşamada mRNA molekülü ribozom organeli aracılığıyla tRNA moleküllerinin antikodon kolları ile etkileşir. Bir tRNA molekülünün antikodon kolundaki üç nükleobaz mRNA molekülünde kendilerine karşılık gelen üç nükleobaz ile sırasıyla birer Watson-Crick çifti oluşturuyorsa, tRNA’nın önceden yüklenmiş olduğu amino asit protein sentezinde kullanılmak üzere taşıyıcısından ayrılır. Bu şekilde tRNA’lar (kendilerine kodon adı verilen) mRNA’daki her üç nükleobaz için ribozoma bir amino asit taşır. Uç uca eklenen amino asitlerden de protein meydana gelir (bkz: Resim 1’in alt yarısı).

Amino asidini ribozomda bırakan bütün tRNA’ların antikodon nükleobazları sırasıyla yan yana dizildiğinde kalıp DNA zincirindeki nükleobaz dizisinin aynısı elde edilmiş olur. Bu bağlamda, DNA’daki ardışık nükleobaz üçlülerine kod adı verilir. Her bir tRNA molekülü sadece tek bir çeşit amino asit ile yüklenebildiği için, DNA’daki kod dizilimi, bir anlamda, ribozomda sentezlenen proteindeki amino asit dizilimini belirlemiş olur. Ya da diğer bir ifadeyle, kalıtsal bilgi DNA’dan mRNA ve tRNA molekülleri aracılığıyla proteine akmış olur. Kalıtsal bilginin hücre içindeki bu tek yönlü akışı moleküler biyolojinin merkezi dogması olarak da bilinir.

Resim 1 – Kalıtsal bilginin hücre içinde akışı [2] : Son satırdaki renkli V, H, L, T, P, E ve K harfleri sırasıyla valin, histidin, lösin, treonin, prolin, glutamat ve lizin amino asitlerinin kısaltmasıdır.

Genetik Kodun Yozluğu

DNA’daki kod adı verilen ardışık nükleobaz üçlülerinin sırası sentezlenen proteinin yapısındaki amino asit dizisini belirlediği için, protein sentezinden sorumlu olan genlerin dört harfli dilinde bütün kelimelerin 3 harf uzunluğunda olduğu söylenebilir. 

Üç harf uzunluğunda olan ve 4 olası harften oluşan toplam 4 x 4 x 4 = 64 tane kelime vardır. Standart genetik kodda bunlardan 3 tanesi protein sentezini durdurmak için kullanır. Kalan 61 kodun her biri ile antikodon kolunda eş nükleobaz dizilimine sahip bir tRNA olması gerekir. Fakat canlıların çoğunda 45’ten az tRNA bulunur. Peki, neden?

tRNA’ların antikodon kollarının 3-boyutlu eğriliği yüzünden kodon – antikodon eşleşmesinde yozluk vardır: antikodonun ilk nükleobazı bazen karşısındaki mRNA nükleobazının Watson-Crick çifti olmasa da tRNA yüklendiği amino asidi protein sentezi için ribozomda bırakabilir [3]. Yani, 3 harf uzunluğundaki genetik kelimelerin ilk harflerindeki değişiklikler bazen kelimelerin (amino asit) anlamlarını değiştirmeyebilir. Bu da kelimelerin başlangıcında kullanılan birbirinden ayırt edilebilir harf sayısının aslında 4’ten küçük olması demektir. 

Mesela, ilk harf için 3 ayırt edilebilir seçenek mümkünse farklı anlama gelen kelime sayısı 3 x 4 x 4 = 48, 2 ayırt edilebilir seçenek mümkünse farklı anlama gelen kelime sayısı 2 x 4 x 4 = 33 olur. Bu da genelde 45’ten az olan tRNA sayısını açıklamaya yeter.

Daha önce her bir tRNA’nın sadece tek bir amino asit ile yüklenebileceğinden bahsedilmişti. Doğada 700’den fazla amino asit olduğu düşünülürse, proteinlerde kullanılan amino asit sayısının eldeki tRNA sayısı ile kısıtlanıp 45 civarına inmesi beklenebilir. Fakat proteinlerde sadece 20 farklı amino asit bulunur! Yani birden fazla tRNA aynı amino asit ile yüklenebilir. 

Üçlü Genetik Kodun Evrimi

Peki, erişilebilir amino asit sayısındaki bolluğa rağmen tRNA – amino asit eşleşmesindeki bu yozluğun sebebi ne olabilir?

Bu soruya makul bir cevap arayabilmek için genetik kodun evrimini anlamaya çalışmak gerekiyor. Öncelikle, genetik işlerge öyle bir şekilde evrilmiş olmalı ki kalıtsal bilginin nükleik asitlerden proteinlere akışı sırasında (varolan çevresel gürültüler sebebiyle) gerçekleşen hatalara tolerans gösterebilsin. Mesela, kalıtsal bilgi aktarımı sırasında tek bir nükleobazda yapılan hataların organizma için ölümcül sonuçları olmamalı. Hatta üçlü bir kodun tek bir nükleobazında yapılan değişiklik o koda karşılık gelen orjinal amino aside mümkün olduğunca benzer kimyasal özelliklerde bir amino asidi kodlamalı. Diğer taraftan, mümkün olduğunca az kaynak harcamak ve mümkün olduğunca çok amino asit kodlamak da genetik işlergenin evriminde sürücü birer rol oynamış olmalı.

Bu şartlar altında en optimum genetik kodun ne olduğu biraz istatistiksel fizik, biraz topolojik matematik ve biraz da klasik enformasyon teorisi kullanılarak bulunabilir: azami 48 tRNA ve asgari hata ile ayırt edilebilecek azami amino asit sayısı 20’dir [4].

Peki, kodon – antikodon eşleşmesinde yozluk olmasaydı ne olurdu? 

Bu durumda tRNA sayısı 64’e, asgari hata ile ayırt edilebilecek azami amino asit sayısı ise 25’e çıkardı [4]. Genetik kodun neden bu şekilde evrilmediği ve 20 amino asitte donduğu ise cevap aranması gereken bir diğer güzel soru. Fakat bunun için moleküler evrimde üçlü genetik kodun da öncesine gitmek gerekebilir.

DNA Öncesi Dünya ve İkili Genetik Kod

tRNA moleküllerinin bir amino asit ile yüklenmesi aminoasil-tRNA sentataz (aaRS) enzimleri sayesinde gerçekleşir. Kendileri de protein sentezinin sonucunda oluşan bu enzimler nükleik asitlerle amino asitler arasındaki eşleşmeyi sağladıkları için aslında protein sentezinin en hayati bileşenidir. Üstelik ilk ortaya çıkışlarının yaşamın üç krallığa ayrılmasından çok daha önceye, hatta DNA öncesi dünyaya gittiği kabul edilmektedir.

aaRS enzimleri her biri 20 amino asidin bir yarısına özgül olan enzimleri içerecek şekilde 2 büyük sınıfa ayrılır. Bu sınıflar arasında herhangi bir yapısal ya da işlevsel benzerlik bulunmaz. Mesela, tRNA moleküllerine bağlanma stratejileri farklıdır. Diğer taraftan, her bir sınıf içinde tüm üyelerce paylaşılan evrimsel olarak korunmuş ortak motifler vardır ki bunlar enzim etkinliğinde önemli roller oynar. Bu yüzden, 2 sınıfın zaman içinde birbirinden bağımsız olarak evrildiği düşünülmektedir.

aaRS enzimlerinin bu ilginç evrimsel geçmişi her biri 10 amino asit kodlayan birbirinden bağımsız 2 genetik kodun DNA öncesi dünyada ayrı ayrı evrilip, daha sonra bir araya gelmiş olabileceği olasılığını akla getirmektedir. Bu arkaik genetik kodlara en makul aday da tRNA moleküllerinin alıcı kolları üzerinde bulunan ve aaRS enzimlerince tanınan birkaç nükleobazlık bağlanma bölgeleridir [5]. 

Alıcı kola zıt doğrultuda konumlanan antikodon kolundaki 3 nükleobaz genetik kodun evrimi sırasında bu bölgelerden kopyalanıp, mevcut yerlerine göçmüş olabilir. Hatta kodon – antikodon eşleşmesinde şu anda yozluk yaratan ilk nükleobaz 2 kodun birleşme sürecinin başlarında sadece ikili bir sınıf ayıracı olarak işlev görmüş olabilir. 

Böyle bir evrimsel senaryo hem kodon – antikodon eşleşmesindeki mevcut yozluğun kaynağını, hem de modern üçlü genetik kodun neden 20 amino asitte donmuş olabileceğini açıklayabildiği için üzerine daha fazla bilimsel araştırma yapılmasını hak ediyor. Üstelik bu senaryoda arkaik genetik kodlar üçlü değil ikili olmalı. Ve teorik olarak biliyoruz ki ikili bir optimum kodda azami tRNA sayısı 4 x 4 =16, asgari hata ile ayırt edilebilecek azami amino asit sayısı ise 11’dir [4].

Kaynaklar

1) Watson, J.D. and Crick, F.H.C. (1953). Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid, Nature, 171 (4356), 737–739. ; Genetical implications of the structure of deoxyribonucleic acid, Nature, 171 (4361), 964–967.

2) Resmin herkesin kullanımına açık kaynağı: https://commons.wikimedia.org/wiki/File:Genetic_code.svg

3) Crick, F.H.C. (1966). Codon—anticodon pairing: The wobble hypothesis. Journal of Molecular Biology. 19 (2): 548–555.

4) Tlusty, T. (2008). Rate-Distortion Scenario for the Emergence and Evolution of Noisy Molecular Codes. Physical Review Letters. 100 (4): 048101. ; Tlusty, T. (2010). Acolorful origin for the genetic code: Information theory, statistical mechanics and the emergence of molecular codes. Physics of Life Reviews. 7: 362–376.

5) Schimmel, P., Giege, R., Moras, D., and Yokoyama, S. (1993). An operational RNA code for amino acids and possible relationship to genetic code. Proc. Natl. Acad. Sci. USA 90: 8763–8768. ; Ribas de Pouplana, L. and Schimmel, P. (2001). Operational RNA Code for Amino Acids in Relation to Genetic Code in Evolution. J. Biol. Chem. 276: 6881–6884. ; Shaul, S., Berel, D., Benjamini, Y., and Graur, D. (2010). Revisiting the operational RNA code for amino acids: Ensemble attributes and their implications. RNA 16: 141–153.

Yazının epiSTEM Türkiye bağlantısı:

https://epistemturkiye.org/genetik-kod-ve-molekuler-evrimi/

Kovalent Bağların İyonikliğinden, Hidrojen Bağlarının Kovalentliğine Kuantum Fiziği - epiSTEM Türkiye

Hidrojen bağları kimyasal olarak epey zayıf, biyolojik olarak ise oldukça önemlidir. Her şeyden önce suyu canlılar için bu kadar hayati ve benzersiz yapan fiziksel özelliklerinin çoğu molekülleri arasındaki hidrojen bağları ile ilgilidir. Ayrıca yeterince zayıf olmaları kendileri üzerinden gerçekleşen etkileşimlere bir esneklik verir ki bu onları hem biyolojik organizasyonda, hem de biyomoleküler tanımada baş tacı yapar. Bu bağlamda benim aklıma ilk gelen genetik malzememiz DNA'da oynadıkları rol: DNA sarmalının çift zincirini bir arada tutan da hidrojen bağlarıdır, DNA'nın bir zincirindeki kalıtsal bilginin okunup protein sentezinde kullanılmasını sağlayan da.

Peki, su ve DNA gibi hidrojen bağlarının merkezi bir rol oynadığı (biyo)kimyasal sistemlerde bu bağlar kurulurken olup biteni elektronların seviyesine inip izlemeyi denesek ne görürdük? Tünelleme, süperpozisyon, dolaşıklık gibi gündelik algılarımızla uyuşmayan kuantum mekaniksel olgularla karşılaşır mıydık? Daha da önemlisi, elektronların bu sistemlerde klasik fiziğin hareket yasalarına göre değil de kuantum fiziğinin yasalarına göre hareket etmesi tekrar biyomoleküler ölçeğe çıktığımızda anlamlı bir fark yaratır mıydı?

Gelin hep beraber bu soruların cevaplarını arayalım. Fakat elektronların davranışları üzerinde kuantum fiziğinin yasalarının belirleyiciliğini ve bunun atomik/moleküler ölçekte karşılığını önce atomlar arasındaki kovalent bağlarda, sonra moleküller arasındaki hidrojen bağlarında inceleyelim.

Kimyasal Bağ 

Atom ya da molekül gibi iki kimyasal birim arasındaki etkileşimde her türlü net çekim kimyasal bir bağ olarak tanımlanabilir. Fakat daha sonra göreceğimiz gibi net kuvvet üzerinden tanım yapmak bazen kafa karıştırıcı olabiliyor. Bu yüzden enerji üzerinden ilkine eşit şöyle alternatif bir tanım geliştirebiliriz: iki kimyasal birim bir araya geldiğinde toplam enerjileri azalıyorsa, yani daha kararlı bir duruma ulaşıyorlarsa, bileşkeleri de bağımsız bir kimyasal birim kabul edilebilir ve aralarındaki kimyasal etkileşim bir bağa karşılık gelir. 

Periyodik tablonun son sütununu dolduran soy gazlar, bütün elektronik orbitalleri dolu olduğu için en kararlı atomlardır. Diğer atomlar da aslında onlarınkine yakın bir elektronik kararlılığa ulaşmak için birbirleriyle bağ yapar. Bu bakımdan doğadaki en yaygın atomik etkileşimlerden birisi kovalent bağdır. Azami kararlılığa ulaşmak için kendince eksik birer elektronu olan iki atom bu iki elektronu çekirdekleri arasında ortaklaşa paylaşarak kovalent bir bağ oluşturabilir. Bakınız Şekil 1. Hidrojen bağlarına geçmeden önce bu bağların fiziğini ayrıntılı bir şekilde ele alacağız. Fakat önce alternatiflerine hızlıca bir göz atalım. 

Şekil 1: Kovalent bağ tasviri 

Genelde kovalent bağlardan biraz daha zayıf olan ve zıt elektrik yüklerin Coulomb kuvveti ile birbirini çekmesine dayanan, yani bir çeşit elektrostatik bağ olan, iyonik bağlar da atomların dünyasında oldukça yaygındır. İki atomun arasında bu tür bir bağın varlığından söz edilebilmesi için özünde yüksüz olan atomların önce zıt yükler ile yüklenerek iyonlaşması gerekir. Atomlardan birisinin kendince elektron eksiği varken diğerinin kendince elektron fazlası varsa, bir atomdan diğerine elektron transferi ile atomların iyonlaşması mümkün olabilir. Bu şekilde elektron kaybeden atom net bir artı yüke, elektron kazanan atom ise net bir eksi yüke kavuşur. Bakınız Şekil 2. Fakat eksik ve fazla elektron sayıları birbirine eşit olan her atom çifti iyonik bağ kuramaz. Çünkü her atomun iyonlaşması için gereken enerji bir değildir. Bazı fazla elektronlu atomlardan elektron koparmak görece kolayken, bazılarına bunu yapmak mümkün bile değildir. 

Şekil 2: İyonik bağ tasviri 

Bunların yanı sıra, bir de birden fazla atom çekirdeğinin net bir artı elektrik yükü gibi merkezde konumlandığı, dış kabuk elektronlarının hepsinin de net bir eksi yük olarak onların etrafında serbest bir şekilde dolaştığı metalik bağlar vardır. Aslında periyodik tablonun çoğunu metallerin doldurduğunu düşünürsek, onların arasında kurulan bu bağlar atomik dünyada en sık rastlanan kimyasal bağ türü olmalı. Fakat hidrojen bağlarını anlamak için - en azından bugün - onlara ihtiyacımız olmayacak. Ama şunu söylemeden geçmeyelim: bu yazının ilerleyen kısımlarında kısmen de olsa göreceğiz ki kovalent, iyonik ve metalik diye yaptığımız bu atomik bağ sınıflandırması aslında çok da katı sınırlar içermemektedir [1]. 

Biraz Kuantum Fiziği 

Şekil 1'deki gibi kovalent bağ tasvirleri zihinsel hijyene yeterince özen gösterilmemesi durumunda yanıltıcı, hatta aldatıcı olabilir. Bu tasvirlerde elektronların orijinal yörüngelerinden hiç ayrılmaması, iki yörüngenin kesişiyor gösterilmesi ve her elektronun bir kesişim noktası üzerinden her iki yörüngeye de dâhil edilmesi oldukça önemlidir. Özellikle de aslında karmaşık üç boyutlu şekillere sahip uzamsal hacimlere karşılık gelen kuantum mekaniksel orbitallerin klasik dairesel yörüngeler ile temsil edilmiş olduğunu düşünürsek. Bunlara dikkat edilmemesi durumunda, ortaklaşa paylaşılan elektron çifti atom çekirdeklerinin fiziksel olarak arasında ve yan yana (ya da üst üste) konumlanıyor gibi tasavvur edilebilir. Bu, ilk bakışta makul bir tasavvur gibi görünebilir: kovalent bağ, ortadaki eksi yüklü elektron çiftinin iki yanında kalan artı yüklü çekirdekleri çekmesinin bir temsili olarak düşünülebilir. Fakat bu tasavvurda büyük bir sorun var: elektron çiftinin bu şekilde konumlanması o kadar yüksek bir enerji gerektirir ki onları bir an bile orada tutmak neredeyse imkânsızdır. Peki, öyleyse kovalent bağda elektronlar tam olarak nasıl paylaşılmaktadır? 

Bu paylaşım klasik bir paylaşım değildir, tamamen kuantum fiziksel bir paylaşımdır. 

Kuantum fiziğinin elektronların atom içinde sadece orbitallerle sınırlı bölgelerde bulunabildiğinin, yani diğer yerlerde elektronun bulunmasının yasak olduğunun keşfi ile doğduğunu duymuş olabilirsiniz. Size bu noktada bir fizikçi sırrı vereyim: doğada karşılaştığımız her yeni yasak daha önce mümkün olacağını hayal bile edemeyeceğimiz bazı şeylerin gerçekleşmesine izin veriyor olabilir. Örneğin bağlı bir elektronun her yerde bulunmasını yasaklayan kuantum fiziği, aslında o elektronun birden fazla izinli yerde aynı anda bulunmasına da izin verebilir. Kovalent bağda paylaşılan elektronların başına gelen de fizikçilerin "kuantum süperpozisyon durumda bulunmak", kimyacıların ise daha çok “rezonans” olarak bildiği bu olgunun tam kendisidir. Bunu isterseniz (Dirac formalizmi diye bilinen bir temsil üzerinden) biraz karikatürleştirerek uzun uzun irdeleyelim. 

Şekil 1 ve 2’deki gibi kimyasal bağ kuracak iki atomu duruma göre X, Y veya Z ile etiketleyelim, üzerinden bağ kurulacak elektronları ise "·" ile gösterelim. Ayrıca, herhangi bir fiziksel durumu "|" ve ">" arasında yazarak temsil edelim. Bu temsilde Şekil 2’de tasvir edilen atomların iyonlaşarak elektrostatik bağ kurduğu süreci şöyle yazabiliriz: 

|X·> |Y> → |X⁺> |(Y·)^-> . 

Elektronun konumunun ölçülmemesi şartıyla, kuantum fiziği yukarıdaki elektron transferinin aynı anda hem gerçekleşmiş, hem de gerçekleşmemiş olmasına izin verebilir. Yani elektronun X ve Y’nin orbitallerinde aynı anda bulunması mümkündür. Böyle bir süperpozisyon durumunu şöyle temsil edebiliriz:

a |X·> |Y> + b |X⁺> |(Y·)^-> . 

Bu yazımda sadece a a* + b b* = 1 şartı bulunmaktadır. Çünkü elektronun konumu ölçüldüğünde bu süperpozisyon çöker ve elektronun a a* olasılıkla X’in orbitalinde, b b* olasılıkla Y’nin orbitalinde olduğu gözlenir.

Kuantum süperpozisyonu bu şekilde örnekledikten sonra Şekil 1’deki X–Z kovalent bağının temsiline geçebiliriz:

|X·> |Z·> → | X–Z > = a | X·–·Z > + b |X⁺> |(Z··)^-> + c |(X··)^-> |Z⁺> , 

a a* + b b* + c c* = 1. Buradaki ilk terim elektronların ortaklaşa paylaşımını anlatmaktadır. Son iki terimin varlığı ise kovalent bağın aslında biraz da, doğrusunu söylemek gerekirse tam olarak b b* + c c* olasılıkla, iyonik karakterde olduğu anlamına gelmektedir. Bağ türleri arasında çok da katı sınırlar yok demiştik ya daha önce, işte bunu kastetmiştik.

Sonunda kovalent bağdaki ortaklaşa elektron paylaşımının ne olduğunu açıklayabilirim size. Yukarıdaki ilk terim tam olarak aşağıdaki şekilde yazılabilir:

| X·–·Z > = d |X·> |Z·> + e |X·> |Z·> , 

d d* + e e* = 1. Yani her iki elektron da aynı anda her iki atomik orbitalde bulunur. Fakat konumlarını ölçmeye kalktığınızda onları asla aynı orbitalde göremezsiniz! d d* olasılıkla elektronlar orijinal atomik orbitallerinde, e e* olasılıkla ise karşı atomların orbitallerinde ölçülürler. Fakat iki elektron aslında özdeş olduğu için sizin ölçüm sonucunuz bunlardan hangisi asla bilemezsiniz. Zira onları gerçek hayatta yukarıdaki gibi kırmızı ve mavi renklerle boyama şansımız bulunmamaktadır.

Kovalent bağdaki elektron çifti paylaşımını gündelik algılarımızla daha uyumlu hale getirmek için, bağlı atomların bireysel orbitalleri üzerinden düşünmek yerine oluşan molekülün kendine özgü yeni orbitallere sahip olacağını varsayabiliriz. Tabii kovalent bağ sonucu zuhur eden moleküler orbitallerin her birisinin özünde mevcut atomik orbitallerin (farklı fiziksel durumlara karşılık gelen) farklı birer kuantum süperpozisyonu olması şartıyla. Bu şekilde iki yeni moleküler orbital tanımlayabiliriz: 1) elektron çiftinin içinde bulunduğu ve atomik orbitallerin enerjilerinden daha düşük enerjili bağlanma orbitali, 2) boş olan ve atomik orbitallerin enerjilerinden daha yüksek enerjili karşıt-bağlanma orbitali. Öyle ki elektronlardan birisine bile enerji verip onu karşıt-bağlanma orbitaline uyarırsanız moleküler yapı kararsızlaşacak, kovalent bağ kırılacak ve atomlar birbirinden ayrılacaktır.

Hidrojen Bağları

Şimdi bileşenlerinden birinin hidrojen olduğu bir X–H kovalent bağına bakalım:

| X–H > = a | X·–·H > + b |X⁺> |(H··)^-> + c |(X··)^-> |H⁺> , 

a a* + b b* + c c* = 1. Hidrojenin çekirdeğinde sadece bir tane proton olması onun elektronları çok zayıf çekmesine sebep olur ve bu yüzden herhangi bir ölçüm sonrasında iki elektronun da onun orbitalinde bulunma olasılığını neredeyse sıfır yapar. Yani aşağıdaki gibi b = 0 olarak kabul edilebilir:

| X–H > = a | X·–·H > + c |(X··)^-> |H⁺> , 

a a* + c c* = 1. Şimdi bu kovalent bağın yanına bir orbitalinde iki tane elektron bulunan, yani temsilen |Y··> durumunda yazılabilen ikinci bir atom yaklaştıralım:

| X–H > |Y··> = a | X·–·H > |Y··> + c |(X··)^-> |H⁺> |Y··> . 

İkinci atomun varlığında kovalent bağdaki elektron dağılımı f f* < a a*, g g* > c c* ve f f* + g g* = 1 olacak şekilde yeniden düzenlenecektir:

| X–H > |Y··> → f | X·–·H > |Y··> + g |(X··)^-> |H⁺> |Y··> . 

Buradaki ilk terim herhangi bir etkileşim tarif etmemektedir. Fakat ikinci terim ortada kısmi artı yüklü hidrojen çekirdeğinin, solda kısmi eksi yüklü X atomunun ve sağda Y atomunun yalnız elektron çiftinin konumlandığı; yani hidrojen çekirdeği üzerinden net bir elektrostatik çekimin gerçekleştiği duruma karşılık gelir. f f* < a a* ve g g* > c c* olduğu için X atomu ve hidrojen arasındaki kovalent bağ biraz uzamış, hidrojen biraz Y atomuna yaklaşmış olmuştur. İşte bu, klasik hidrojen bağının tanımı olarak verilebilir. Çoğu kişi de hidrojen bağlarının bu tanım ile sınırlı olduğunu sanmaktadır. Fakat bu bağların kuantum fiziği üzerine konuşmaya daha hiç başlamadık bile.

Şekil 1'deki kovalent bağ tasvirinde yörüngelerin kesişmesi atomik orbitallerin örtüşmesini temsil ediyordu. Elektron paylaşımına izin veren ve moleküler orbital tasavvuruna meşru bir zemin sağlayan da bu örtüşmeydi. Benzer şekilde hidrojen bağlarında X–H molekülünün boş olan karşıt-bağlanma orbitali ile Y atomunun yalnız elektron çiftinin atomik orbitali de örtüşebilmektedir. Bu örtüşme sonucu yalnız elektron çifti kendilerinin orjinal Y atomu orbitali ile X–H molekülünün karşıt-bağlanma orbitalinin bir kuantum süperpozisyon durumunda bulunabilecektir. Yani aynı anda hem ikisi birden oldukları yerde kalabilecek, hem de birisi X–H molekülünün karşıt-bağlanma orbitaline transfer edilebilecektir. Bunu şu şekilde karikatürleştirebiliriz:

| X–H > |Y··> → h | X·–·H > |Y··> + j |(X··)^-> |H⁺> |Y··> + k | (X·–·–·H)^- > |(Y·)⁺> , 

h h* + j j* + k k* = 1. Bu süperpozisyondaki ilk ve son terimin birlikte varoluşu hidrojen bağının doğasının kısmen kuantum fiziksel olması anlamında "hidrojen bağının kovalentliği" olarak adlandırılan olgudur. Bu olgunun ilk deneysel gösterimi su buzundaki hidrojen bağları incelenerek yapıldı ve 1999 yılında Physical Review Letters dergisinde yayınlanandı [2]. Aynı yıl yayınlanan bir kuantum kimya hesabı sonucuna göre de DNA çift zincirini bir arada tutan hidrojen bağlarında net bir çekici etkileşim olmasının hidrojen bağlarının kovalentliği olmaksızın açıklanamayacağı iddia edildi [2]. Bu iddia da, hidrojen bağlarının kovalentliğinin kapsamı da o günden beri kuantum kimyacılar arasında tartışılmaya devam ediyor. Özellikle ikincisi için güzel bir özet Kaynak [3]'te bulunabilir.

Yazıyı dikkatli okuyanların gözünden kaçmış olamaz, X–H molekülünün karşıt-bağlanma orbitalindeki elektron varlığı X atomu ile hidrojen arasındaki kovalent bağı kırma potansiyeline sahiptir. Peki, bu kırılma gerçekleşirse ne olur, yine de kararlı bir hidrojen bağı kurulabilir mi?

Hidrojen atomunun çekirdeğini oluşturan proton X ve Y atomlarına ayrı ayrı kovalent olarak bağlı olma durumlarının kuantum süperpozisyonunda bulunursa neden olmasın. Üstelik proton bu süperpozisyon durumunda bulunması hidrojen bağlarının biyokimyasal sistemlerdeki önemli rolünü daha önce hayal edilemeyecek ölçüde genişletebilir. Bunlar için Kaynak [5] ve [6]'da özetlemeyi denediğim araştırmalarıma bakabilir, bu konuda aklınıza takılan herhangi bir şeyi tartışmak için de hiç tereddüt etmeden bana ulaşabilirsiniz.

Şimdilik burada duralım en iyisi.

Efendim, bilimle kalın, bize katılın,,

Kaynaklar

1) Pauling, L. (1960). The nature of the chemical bond and the structure of molecules and crystals: An introduction to modern structural chemistry, Cornell University Press, 3rd edition.

2) Isaacs, E., Shukla, A., Pltazman, P.M., Hamann, D.R., Barbiellini, B. and Tulk, C.A. (1999). Covalency of the hydrogen bond in ice: a direct x-ray measurement, Physical Review Letters, 82(3), 600–603.

3) Fonseca Guerra, C., Bickelhaupt, F.M., Snijders, J.G. and Baerends, E.J. (1999). The nature of the hydrogen bond in DNA base pairs: The role of charge transfer and resonance assistance, Chemistry - A European Journal, 5(12), 3581–3593.

4) Grabowski, S.J. (2011). What Is the Covalency of Hydrogen Bonding?, Chemical Reviews, 111(4), 2597–2625.

5) Pusuluk, O., Farrow, T., Deliduman, C. and Vedral, V. (2018). Emergence of correlated proton tunneling in water ice, arXiv/quant-ph, 1703.01335v2, https://arxiv.org/abs/1703.01335v2.

6) Pusuluk, O., Farrow, T., Deliduman, C., Burnett, K. and Vedral, V. (2018). Proton tunneling in hydrogen bonds and its implications in an induced-fit model of enzyme catalysis, arXiv/physics.chem-ph, 1703.00789v2, https://arxiv.org/abs/1703.00789v2.

Yazının epiSTEM Türkiye bağlantısı:

https://epistemturkiye.org/kovalent-baglarin-iyonikliginden-hidrojen-baglarinin-kovalentligine-kuantum-fizigi/